경로탐색(DFS, 인접행렬)

01 May 2023 in Algorithm on Java, Coding, Test

문제

방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프 로그램을 작성하세요. 아래 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는

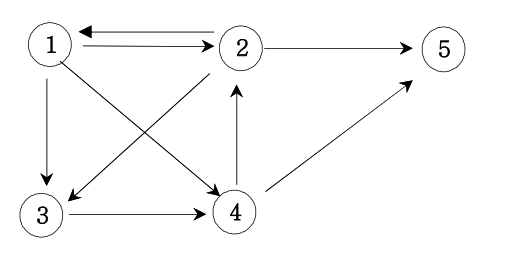
12345 125 13425 1345 1425 145

총 6 가지입니다.

입력

첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연 결정보가 주어진다.

출력

총 가지수를 출력한다.

입력예제

5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5

출력예제

6

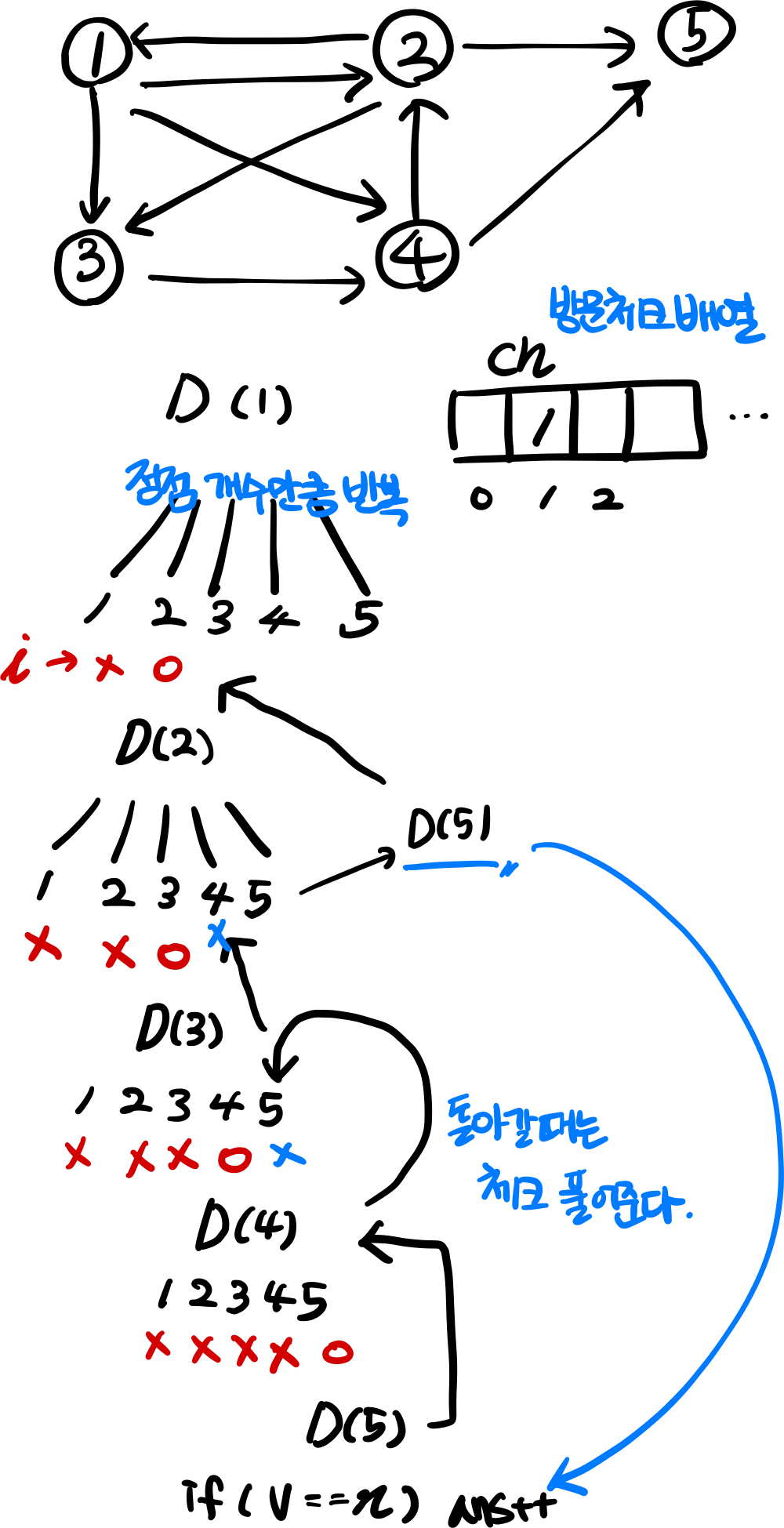
해결방법

• 시작 정점으로 재귀함수 시작
• 시작 후, 노드 개수 만큼 반복하여 갈 수 있는 곳으로 재귀함수 호출
• 재귀 함수 호출 전, 방문 체크 하고 호출 후 끝나면 방문 체크를 해제한다
• 목적지에 도착하면 방문 가지 수를 구하기 때문에 +1 한다.
• 만약, 도착 케이스의 방문 노드를 구하는 것이면 거쳤던 체크 배열을 통해 원래 노드를 가져온다.

코드

import java.util.*;

class Main {
    static int n, m, answer = 0;
    static int[][] graph;
    static int[] ch;

    public void DFS(int v) {
        // 파라미터가 정점의 수와 같으면 정답 ++ 
        if (v == n) answer++;
        else {
            // 정점의 개수 만큼 반복
            for (int i = 1; i <= n; i++) {
                // 해당 그래프의 정점을 방문하지 않은 경우에만 진행
                if (graph[v][i] == 1 && ch[i] == 0) {
                    // 방문 했다고 체크하고
                    ch[i] = 1;
                    // 다음을 진행.
                    DFS(i);
                    // 그리고 체크를 품.
                    ch[i] = 0;
                }
            }
        }
    }

    public static void main(String[] args) {
        Main.Main T = new Main.Main();
        Scanner kb = new Scanner(System.in);
        n = kb.nextInt();
        m = kb.nextInt();
        // 배열로 그래프 생성
        graph = new int[n + 1][n + 1];
        ch = new int[n + 1];
        // 그래프 값 바인딩
        for (int i = 0; i < m; i++) {
            int a = kb.nextInt();
            int b = kb.nextInt();
            graph[a][b] = 1;
        }
        // 체크 배열 생성
        ch[1] = 1;
        T.DFS(1);
        System.out.println(answer);
    }
}