다익스트라 알고리즘

04 Jun 2023 in Algorithm on Java, Coding, Test

다익스트라 알고리즘

문제

아래의 가중치 방향그래프에서 1번 정점에서 모든 정점으로의 최소 거리비용을 출력하는 프로 그램을 작성하세요. (경로가 없으면 Impossible를 출력한다)

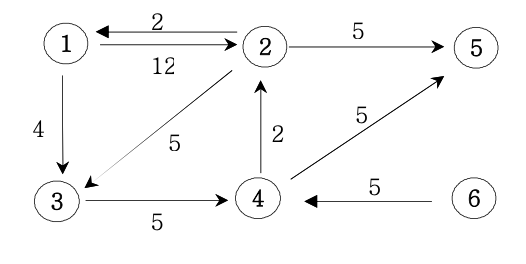
설명

첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연 결정보와 거리비용이 주어진다.

출력

1번 정점에서 각 정점으로 가는 최소비용을 2번 정점부터 차례대로 출력하세요.

입력 예제 1

6 9
1 2 12 // 1번 정점에서 2번정점으로 가는데 12의 비용이 든다. 
1 3 4 
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2 
4 5 5
6 4 5

출력 예제 1

2 : 11
3 : 4
4 : 9
5 : 14
6 : impossible

해결방법

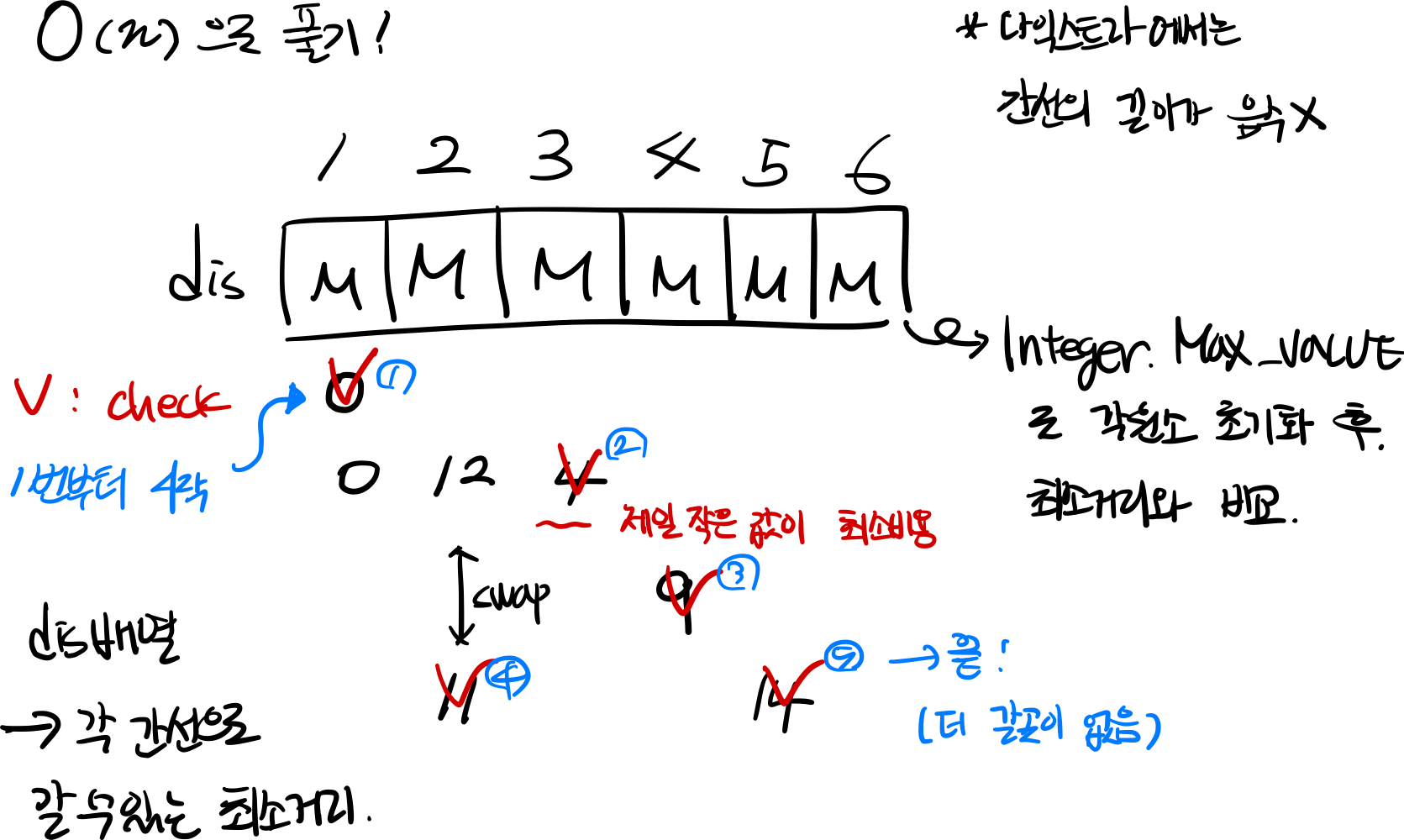
• 위 메모는 O(n)으로 푸는 방식을 설명한 그림. 다익스트라와 비슷하나 for문 도는 것 자체가 비용이 엄청나게 듬
• 따라서, 이를 해결하기 위한 방법으로 우선순위 큐를 사용하는 다익스트라 알고리즘을 사용하여 문제를 해결
• 다익스트라 알고리즘에서는 각 간선으로 가는 비용이 음수가 될 수 없음.

코드

import java.util.*;

// 간선 객체 생성
class Edge implements Comparable<Edge> {
  // 정점과 비용(가중치)을 저장
  public int vex;
  public int cost;

  Edge(int vex, int cost) {
    this.vex = vex;
    this.cost = cost;
  }

  @Override
  public int compareTo(Edge ob) {
    return this.cost - ob.cost;
  }
}

class Main {
  static int n, m;
  static ArrayList<ArrayList<Edge>> graph;
  static int[] dis;

  public void solution(int v) {
    PriorityQueue<Edge> pQ = new PriorityQueue<>();
    // 첫번째 시작 정점 삽입
    pQ.offer(new Edge(v, 0));
    // 시작 정점은 최소거리 0으로 초기화
    dis[v] = 0;
    // 다익스트라 시작.
    while (!pQ.isEmpty()) {
      // 큐에서 하나 꺼냄.
      Edge tmp = pQ.poll();
      // 현재 정점과 비용 대입.
      int now = tmp.vex;
      int nowCost = tmp.cost;
      // 현재 꺼낸 정점 비용이 해당 정점 최소 비용보다 큰 경우 통과
      if (nowCost > dis[now]) continue;
      // 비교 시작.
      // 현재 정점에서 갈 수 있는 정점 배열 꺼내서 반복
      for (Edge ob : graph.get(now)) {
        // 다음 정점으로 가는 비용(현재비용 + 다음 정점 가는 비용)이
        // 해당 정점으로 가는 비용보다 작은 경우 (최소값인 경우)
        if (dis[ob.vex] > nowCost + ob.cost) {
          // 해당 정점으로 가는 비용을 다음 정점 가는 비용으로 교체
          dis[ob.vex] = nowCost + ob.cost;
          // 교체했다는 것은 갈 수 있으므로 전진한다. 는 의미이므로
          // 큐에 해당 정점 가는 객체 저장
          pQ.offer(new Edge(ob.vex, nowCost + ob.cost));
        }
      }
    }
  }

  public static void main(String[] args) {
    Main T = new Main();
    Scanner kb = new Scanner(System.in);
    n = kb.nextInt();
    m = kb.nextInt();
    // 각 정점이 갈 수 있는 간선을 가지고 있는 배열 객체를 저장하는 그래프 배열 객체.
    graph = new ArrayList<ArrayList<Edge>>();
    for (int i = 0; i <= n; i++) {
      // 간선 객체 초기화
      graph.add(new ArrayList<Edge>());
    }
    // 각 정점으로 갈 수 있는 최소비용을 저장하는 배열 초기화
    dis = new int[n + 1];
    // 해당 배열을 최대값으로 초기화(최소 비용을 비교해서 저장해야 하므로)
    Arrays.fill(dis, Integer.MAX_VALUE);
    // 정점과 간선 비용 대입
    for (int i = 0; i < m; i++) {
      // 그래프 정점
      int a = kb.nextInt();
      // 그래프 정점에서 갈 수 있는 정점
      int b = kb.nextInt();
      // 그 정점으로 가는 비용
      int c = kb.nextInt();
      // 위 값으로 객체 삽입
      graph.get(a).add(new Edge(b, c));
    }
    // 수행.
    T.solution(1);
    // 2번 정점 부터 찍는다. 만약 배열에 최대값이 초기화 되지 않고 있다면 가는게 불가능 하므로
    // 불가능을 찍는다.
    for (int i = 2; i <= n; i++) {
      if (dis[i] != Integer.MAX_VALUE) System.out.println(i + " : " + dis[i]);
      else System.out.println(i + " : impossible");
    }
  }
}